As smart as we as a species are, Mother Nature almost always seems to have us beat. It’s true for things like brain surgery and robotics; it’s true for the race to swerve the heat death of the planet; and, apparently, it’s also true for advanced math.

“A central problem of geometry is the tiling of space with simple structures,” begins a new paper, published this week by researchers at the University of Oxford and reporting the discovery of a brand-new class of shapes named soft cells. 

“The classical solutions, such as triangles, squares, and hexagons in the plane and cubes and other polyhedra in three-dimensional space are built with sharp corners and flat faces,” the authors write. “However, many tilings in Nature are characterized by shapes with curved edges, nonflat faces, and few, if any, sharp corners.”

Basically, the problem is this: how do we best completely fill a space with shapes or objects? When you set this question to humans, we instinctively go for sharp-cornered shapes – squares, triangles, hexagons, those kinds of things. It makes sense – after all, try to fill a space with circles, and you will necessarily end up with some empty bits, regardless of how small or intricately you pack them.

But when we look to how the natural world has answered the question, it’s exceedingly rare to see this type of solution. As Alain Goriely, Professor of Mathematical Modelling at the University of Oxford and one of the authors of the new paper, puts it: “Nature not only abhors a vacuum, she also seems to abhor sharp corners.”

Consider, for example, an onion. Cut it in half, and you’ll see a perfectly packed collection of interlocking shapes, but certainly no right angles or straight lines. It’s the same with muscle tissue: a cross-section of the cells that make up smooth muscle fibers will reveal a tessellation of squidged-out circles, long and thin, with points at either end.

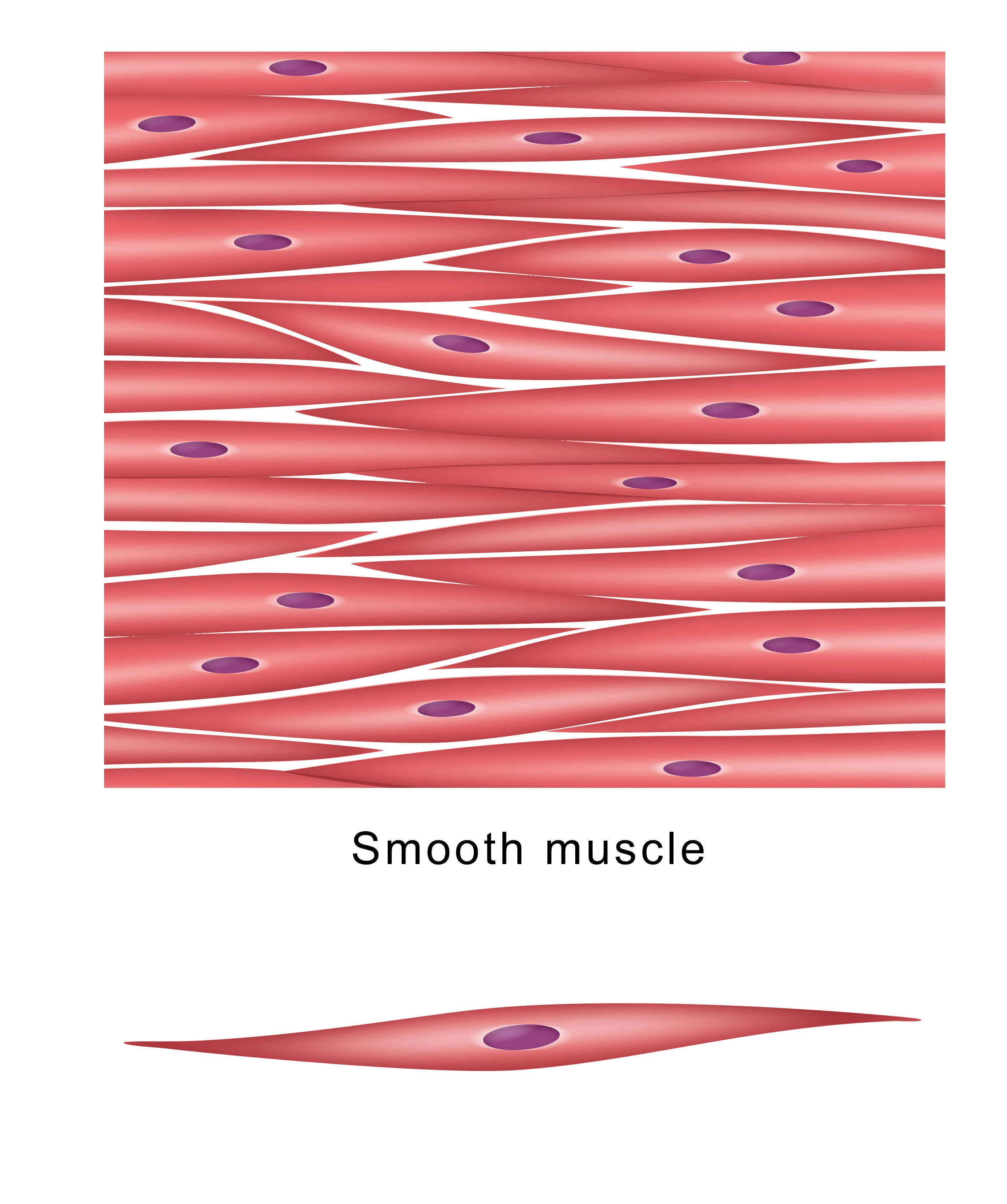
Now, it’s not as if nobody ever noticed that these shapes existed before – or that they’re a neat way to fill an area with no empty space left over. But exactly how they work from a mathematical point of view? That’s been a bit of a puzzle.

“While the combinatorial properties of tilings have been investigated in detail, less attention was paid to the smoothness of the cells,” the paper explains. “Since piecewise smooth shapes, such as squares and cubes, do fill space, and smooth shapes do not, a natural question is how smooth space-filling shapes can be.”

It’s a little technically complex, but it boils down to this: if a shape isn’t "pointy" enough, then there’s just no way for it to successfully fill a space. The question the team needed to answer, therefore, is how pointy a shape needs to be at minimum, in order to successfully tile a space.

The solution, they discovered, are these “soft cells”. These are shapes which “minimiz[e] the number of sharp corners,” they explain in the paper, “filling space as soft tilings […] Remarkably, these ideal soft shapes, born out of geometry, are found abundantly in nature, from cells to shells.”

These shapes are particularly interesting once we move up from two to three dimensions. “Soft cells help explain why, when you look at a cross section of a chambered shell, it shows corners but the 3D geometry of the chambers doesn't,” explains Gábor Domokos, Professor of Geometric Modeling, Budapest University of Technology and Economics and one of the paper’s authors.

Indeed, as with so many dramatic revelations, these shapes can be found everywhere once you know what to look for. They are “geometric building blocks of biological tissue,” the team explain, governing such ubiquitous natural forms as tip growth, blood cells, river islands, and seashells.

“Establishing and maintaining sharp corners in physical cells is difficult and costly,” the researchers write, “as surface tension and elasticity naturally tend to smooth corners. Hence, it is not surprising that many soft tilings are found in Nature.”

“The lack of sharp corners and their soft, highly curved geometry makes soft cells ideal candidate models for biological structures which evolved under full or partial constraint to fill space,” they conclude.

The paper is published in the journal PNAS Nexus.